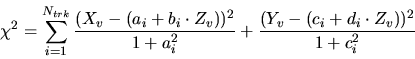Next: 2nd track finding :
Up: Analysis flow
Previous: Variables for combinatorial backgrounds
Contents
Figure 3:
Various type of vertices defined in the scifi tracker
 |
- The intersection of two(or more) tracks
(Fig. 3(a),(b))
- Find the intersection of two or more 3D tracks
- For
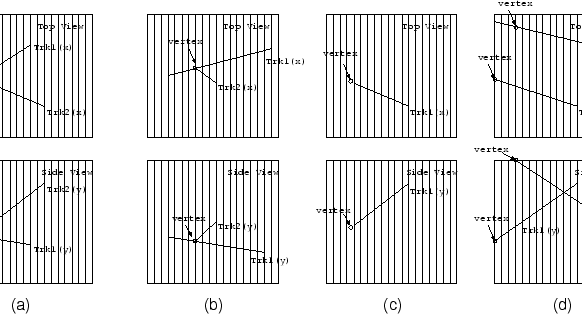
 , i-th track :
, i-th track :
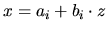 /
/
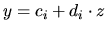
- Vertex position(
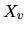 ,
,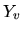 ,
,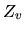 ) as a fitting parameter
) as a fitting parameter
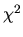 is defined as
is defined as
- Find (
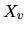 ,
,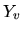 ,
,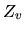 ) to minimize
) to minimize 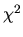
- If
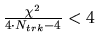 , (
, (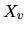 ,
,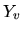 ,
,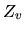 )
will be a vertex which has
)
will be a vertex which has 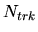 -associated tracks.
-associated tracks.
- Then, the fine fitting is performed to get the better vertex
position(
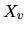 ,
,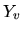 ,
,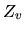 ) and
) and 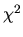 . Here, the track
parameter(
. Here, the track
parameter(
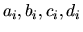 ) as well as the vertex
position(
) as well as the vertex
position(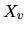 ,
,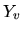 ,
,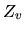 ) will be considered as fitting parameter. [2]
) will be considered as fitting parameter. [2]
- For single track(which doesn't intersect with other
tracks), the extrapolated point to the mid of the closest water
tank of the track. (See Fig. 3(c))
- For the track of Fig. 3(c) which starts at 5th layer
of SciFi :
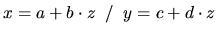
- The mid point of the water target( locates between 4th and 5th
SciFi layer) :
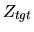
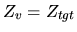 ,
,
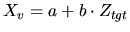 , and
, and
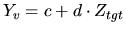 .
.- If vertex is located inside SciFi volume,
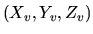 will be
a vertex which has one associated tracks.
will be
a vertex which has one associated tracks.
- For the entering track to the scifi volume, the entering
point. (See Fig. 3(d))
- At the step '2 (c)', if vertex is located outside SciFi volume,
Find the entering point of track.
- In the case of Trk1 of Fig. 3, the track enters
from the front of SciFi detector and the vertex will be the track start
point, i.e. this case, the 1st layer hit of track.
- In the case of Trk2 of Fig. 3, the track enters
from the top of SciFi detector and the vertex will be on the top-side
boundary of SciFi detector. So,
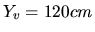 and
and
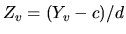 ,
,
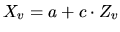 .
.




Next: 2nd track finding :
Up: Analysis flow
Previous: Variables for combinatorial backgrounds
Contents
K2K experimant account
2000-02-09